We survey recent results on the multiplicity of T-periodic solutions of differential systems of the form
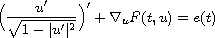
when
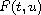 is
is
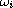 -periodic
with respect to
-periodic
with respect to
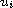
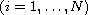 .
Several techniques of critical point theory are used.
.
Several techniques of critical point theory are used.
Jean Mawhin
Abstract:
We survey recent results on the multiplicity of T-periodic solutions
of differential systems of the form
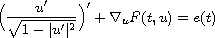
when
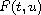 is
is
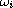 -periodic
with respect to
-periodic
with respect to
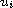
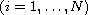 .
Several techniques of critical point theory are used.
.
Several techniques of critical point theory are used.
Published March 21, 2016.
Math Subject Classifications: 34C15, 34C25, 58E05.
Key Words: Pendulum-type equations; multiple solutions; critical point theory;
Ljusternik-Schnirelmann category.
Show me the PDF file (248K), TEX file for this article.
 |
Jean Mawhin Institut de Recherche en Mathématique et Physique Université Catholique de Louvain 1348 Louvain-la-Neuve, Belgium email: jean.mawhin@uclouvain.be |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page