The paper deals with the existence of at least one (weak) solution for a wide class of one-parameter subelliptic critical problems in unbounded domains
 of a Carnot group
of a Carnot group
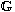 ,
which present several
difficulties, due to the intrinsic lack of compactness.
More precisely, when the real parameter is sufficiently small,
thanks to the celebrated symmetric criticality principle of Palais,
we are able to show the existence of at least one nontrivial solution.
The proof techniques are based on variational arguments and on a recent
compactness result, due to Balogh and Kristaly in [2].
In contrast with a persisting assumption in the current literature we do
not require any longer the strongly asymptotically contractive condition
on the domain
,
which present several
difficulties, due to the intrinsic lack of compactness.
More precisely, when the real parameter is sufficiently small,
thanks to the celebrated symmetric criticality principle of Palais,
we are able to show the existence of at least one nontrivial solution.
The proof techniques are based on variational arguments and on a recent
compactness result, due to Balogh and Kristaly in [2].
In contrast with a persisting assumption in the current literature we do
not require any longer the strongly asymptotically contractive condition
on the domain
 .
A direct application of the main result in the
meaningful subcase of the Heisenberg group is also presented.
.
A direct application of the main result in the
meaningful subcase of the Heisenberg group is also presented.

