2021 UNC Greensboro PDE Conference.
Electron. J. Diff. Eqns., Conference 26 (2022), pp. 151-169.
On solutions arising from radial spatial dynamics of some semilinear elliptic equations
Dario A. Valdebenito
Abstract:
We consider the semilinear elliptic equation
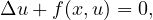
where
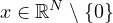 , N≥2, and f satisfies certain
smoothness and structural assumptions. We construct solutions of the form
, N≥2, and f satisfies certain
smoothness and structural assumptions. We construct solutions of the form
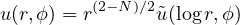 ,
where r=|x|>0,
,
where r=|x|>0,
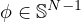 ,
and
,
and
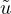 is quasiperiodic in its first
argument with two nonresonant frequencies.
These solutions are found using some recent developments in the theory
of spatial dynamics, in which the radial variable r takes the role of time,
combined with classical results from dynamical systems and the KAM theory.
is quasiperiodic in its first
argument with two nonresonant frequencies.
These solutions are found using some recent developments in the theory
of spatial dynamics, in which the radial variable r takes the role of time,
combined with classical results from dynamical systems and the KAM theory.
Published August 25, 2022.
Math Subject Classifications: 35B08, 35B15, 35J61, 37J40.
Key Words: Semilinear elliptic equations; quasiperiodic solutions;
center manifold theorem; radial spatial dynamics.
DOI: https://doi.org/10.58997/ejde.conf.26.v1
Show me the PDF file (412 K),
TEX file for this article.
Darío A. Valdebenito
Department of Mathematics
Ave Maria University
5050 Ave Maria Blvd
Ave Maria, FL 34142, USA
email: dario.valdebenito@avemaria.edu
|
Return to the table of contents
for this conference.
Return to the EJDE web page
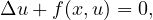
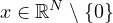 , N≥2, and f satisfies certain
smoothness and structural assumptions. We construct solutions of the form
, N≥2, and f satisfies certain
smoothness and structural assumptions. We construct solutions of the form
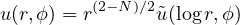 ,
where r=|x|>0,
,
where r=|x|>0,
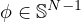 ,
and
,
and
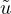 is quasiperiodic in its first
argument with two nonresonant frequencies.
These solutions are found using some recent developments in the theory
of spatial dynamics, in which the radial variable r takes the role of time,
combined with classical results from dynamical systems and the KAM theory.
is quasiperiodic in its first
argument with two nonresonant frequencies.
These solutions are found using some recent developments in the theory
of spatial dynamics, in which the radial variable r takes the role of time,
combined with classical results from dynamical systems and the KAM theory.