Special Issue in honor of Alan C. Lazer.
Electron. J. Diff. Eqns., Special Issue 01 (2021), pp. 239-253.
Connected components of positive solutions of biharmonic equations with the
clamped plate conditions in two dimensions
Ruyun Ma, Zhongzi Zhao, Dongliang Yan
Abstract:
This article concerns the clamped plate equation

where
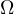 is a bounded domain in
is a bounded domain in
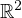 of class
of class
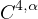 ,
,
 ,
,
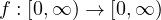 is a locally
Hölder continuous function with exponent
is a locally
Hölder continuous function with exponent
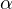 , and
, and
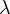 is a positive parameter.
We show the existence of S-shaped connected component of positive solutions under suitable
conditions on the nonlinearity. Our approach is based on bifurcation techniques.
is a positive parameter.
We show the existence of S-shaped connected component of positive solutions under suitable
conditions on the nonlinearity. Our approach is based on bifurcation techniques.
Published November 03, 2021.
Math Subject Classifications: 35J40, 35G30, 35B32, 35P30.
Key Words: Biharmonic operator; positive solutions; eigenvalue; bifurcation.
DOI: https://doi.org/10.58997/ejde.sp.01.m1
Show me the PDF file (387 K),
TEX file for this article.
 |
Ruyun Ma
School of Mathematics and Statistics
Xidian University, Xi'an 710071, China
email: ryma@xidian.edu.cn
|
|---|
 |
Zhongzi Zhao
School of Mathematics and Statistics
Xidian University, Xi'an 710071, China
email: 15193193403@163.com
|
|---|
 |
Dongliang Yan
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: yhululu@163.com
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page

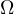 is a bounded domain in
is a bounded domain in
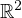 of class
of class
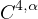 ,
,
 ,
,
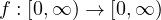 is a locally
Hölder continuous function with exponent
is a locally
Hölder continuous function with exponent
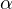 , and
, and
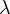 is a positive parameter.
We show the existence of S-shaped connected component of positive solutions under suitable
conditions on the nonlinearity. Our approach is based on bifurcation techniques.
is a positive parameter.
We show the existence of S-shaped connected component of positive solutions under suitable
conditions on the nonlinearity. Our approach is based on bifurcation techniques.


